Optimal indexing of database tables can be achieved using the Texpress configuration subsystem1. A suite of tools is provided for checking the efficiency of configurations and for generating new configurations. It is also possible to save configurations on a per table basis so that settings are not lost with the next automated reconfiguration.
The first part of what follows is a fairly technical explanation of the Texpress indexing mechanism; while challenging, it may prove useful when performing the final (optional) Step 7: Save configuration settings when optimizing Texpress. Your configuration parameters are stored in a params file, and Part 1 of this document explains in detail how the various elements of the params file are calculated.
In the second part, Configuration tools, you will find important information about the configuration tools available for optimizing and configuring the database engine:
The configuration tools that provide optimal indexing for Texpress tables were overhauled with Texpress 8.2.01.
Due to the simplistic approach to automatic configuration taken by earlier versions of Texpress, achieving optimal performance for a table was a bit of a black art. As a result less than optimal performance was noticed, particularly for very large data sets. In many instances manual configuration was the only way to get near optimal performance. Most configuration issues resulted from assumptions that were applicable for data sets with a normal distribution of record sizes, but which did not hold for the diverse data sets found in a "normal" EMu installation. In particular, where data was loaded from a number of disparate legacy systems, the distribution of record sizes did not follow a single normal distribution but resembled a number of normally distributed data sets, one per legacy system, overlaying each other. The histogram below shows the distribution of record sizes for the Parties module:
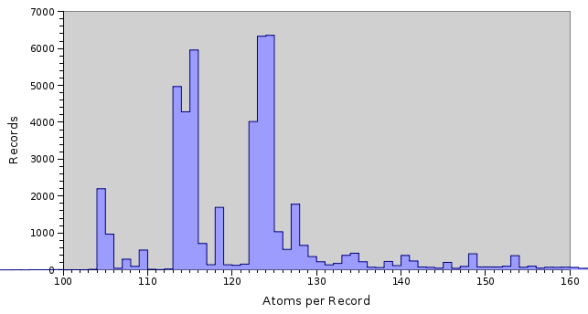
As you can see the distribution of record sizes does not follow a normal distribution. However if you look closely you will notice the histogram is made up of three normal distributions, with centres at 105, 115 and 125, superimposed on each other. Each of these distributions reflects data from a legacy system, so in fact we have three different data sources where each data source is distributed normally, but the combined data set is not!
Prior to Texpress 8.2.01 the automated configuration tools assumed that the data set followed a normal distribution and produced indexes based around this assumption. The end result was that for non normal distributed data sets poor indexing parameters were used, leading to slow response times and excessive false matches. The overhauled configuration facility provided with Texpress 8.2.01 caters for all distributions of data sets while still providing optimal querying speed with minimum disk usage.
What follows is a detailed look at the input parameters to the configuration process as a solid understanding of these values allows targeted manual configuration if it should be required. First of all we need to start with the basics.
Texpress uses a Two Level Superimposed Coding Scheme for Partial Match Retrieval as its primary indexing mechanism. Here we explore what we mean by Superimposed Coding Scheme and look at the variables that affect optimal configuration.
The scheme is made up of two parts: the first is a coding scheme, and the second is the superimposing mechanism. In order to demonstrate how these strategies function, a working example will be used. For the example we will assume we have a simple Parties record with the following data:
|
Field Name |
Value |
|---|---|
| First Name | Boris
|
| Surname | Badenov
|
| City | FrostBite Falls
|
| State | Minnesota
|
Coding Scheme
The first part of the indexing algorithm involves encoding each of the field values into a bit string, that is a sequence of zero and one bits. Two variables are used when encoding a value. The first is k, which is the number of 1s we require to be set for the value and the second is b, which is the length of the bit string. The variables b and k are the first two inputs into the configuration of the indexing mechanism.
To encode a value we use a pseudo random number generator. We need to call the generator k times where the resulting value must be between 0 and b - 1. For each number generated we convert the bit position to a 1. The important feature of a pseudo random number generator is that if we provide the same inputs (that is the same k, b and value), then the same k numbers will be generated, thus the same inputs will always produce the same outputs. Suppose we use k=2 and b=15 to encode our sample record. The table below shows example bit strings generated for the given b and k values:
| Value |
Bit Positions |
Bit String |
|---|---|---|
Boris
|
3, 10 | 00010 00000 10000 |
Badenov
|
1, 4 | 01001 00000 00000 |
FrostBite
|
3, 7 | 00010 00100 00000 |
Falls
|
8, 14 | 00000 00010 00001 |
Minnesota
|
4, 9 | 00001 00001 00000 |
Notice how the two words in the City field are encoded separately. It is this separate encoding that provides support for word based searching, that is searching where only a single word is specified. The pseudo random number generator used by Texpress also takes one other input, the column number of the value being indexed. The reason for this input is that the same word in different columns should result in different bit strings, otherwise a search for the word would find it in all columns (this is how the Also Search facility is implemented, where each Also Search column uses the same column number, that of the originating column).
Superimposed Scheme
Once all the bit strings are generated they are OR-ed together to produce the final bit string. The bit string is known as a record descriptor as it contains an encoded version of the data in the record, in other words it describes the contents of the record in the form of a bit string. Using our example the resulting record descriptor would be:
|
00010 00000 10000 |
OR |
|
01001 00000 00000 |
|
|
00010 00100 00000 |
|
|
00000 00010 00001 |
|
|
00001 00001 00000 |
|
|
01011 00111 10001 |
|
False Matches
The indexing scheme used by Texpress can indicate that a record matches a query when in fact it does not. These false matches are due to the encoding mechanism used. When a query is performed the query term is encoded into a bit string as described above. The resulting record descriptor, generally known as a query descriptor, is AND-ed with each record descriptor and where the resultant descriptor is the same as the query descriptor, the record matches (that is, the record descriptor has a 1 in every position the query descriptor has a 1). Using our example above, let's assume we are searching for the term Boris. We encode the term and compare it against the record descriptor:
|
00010 00000 10000 |
AND |
( |
|
01011 00111 10001 |
|
(Record descriptor) |
|
00010 00000 10000 |
|
(Resultant descriptor) |
Since the resultant descriptor is the same as the query descriptor the record is flagged as a match. Now let's consider searching for Natasha. In order to demonstrate a false match, let's assume Natasha is encoded as follows:
| Value |
Bit Positions |
Bit String |
|---|---|---|
|
|
7, 9 |
00000 00101 00000 |
When we perform our search we get:
|
00000 00101 00000 |
AND |
( |
|
01011 00111 10001 |
|
(Record descriptor) |
|
00000 00101 00000 |
|
(Resultant descriptor) |
As you can see the query descriptor is the same as the resultant descriptor so it looks like the record matches, except that the record for descriptor 01011 00111 10001 does not contain Natasha. This is known as a false match. In order to "hide" false matches from users, Texpress checks each record before it is displayed to confirm that the record does indeed contain the specified search term(s); if not, the record is removed from the set of matches.
The reason for false matches is that a combination of the bits set for a series of terms in a record results in 1s appearing in the same positions as for a single term. Using our example you can see that Frostbite sets bit seven and Minnesota contributes bit nine, which happen to correspond to the bits set by Natasha. In order to provide accurate searching we need to minimize the number of false matches.
Calculating k and b
Now that we have had a look at how the superimposed coding scheme works, that is by translating the contents of a record into a record descriptor, we need to investigate how to calculate k (number of bits to set to 1s per term) and b (length of the bit string). The first variable we will look at is k. In order to calculate k we need to introduce two new variables:
|
d |
The bit density is the ratio between the number of 1 bits set and the length of the descriptor. The value is expressed as a percentage. For example a bit density of 25% indicates that one in four bits will be 1 with the other three being zero when averaged over the whole record descriptor. If we use our example record descriptor of 01011 00111 10001, there are eight 1 bits set out of a total of 15 bits, which gives a bit density of 8/15 or 53%. Texpress uses a default bit density value of 25%. |
|
f |
The false match probability is the number of record descriptors we need to examine to get a false match. For example, a value of 1024 indicates that we expect to have one false match for every 1024 record descriptors checked when searching. Using this variable we can configure the system to provide an "acceptable" level for false matches. Texpress uses a value of 1024 for the false match probability for record descriptors. |
The number of bits we need to set for a term is related to both the false match probability and the bit density. If we use a bit density of 25%, one in four bits is set to 1 in our record descriptor. This implies the probability of any given bit being a 1 is 1/4. If we set k to be 1, that is we set one bit per term, the probability that the bit is already set is 1/4. If we set two bits (k=2), the probability that both bits are set is 1/4 * 1/4 = 1/16. The table below gives more details:
|
k |
Probability all bits set to one |
Value |
|---|---|---|
| 1 | 1/4 | 1/4 |
| 2 | 1/4 * 1/4 | 1/16 |
| 3 | 1/4 * 1/4 * 1/4 | 1/64 |
| 4 | 1/4 * 1/4 * 1/4 * 1/4 | 1/256 |
| 5 | 1/4 * 1/4 * 1/4 * 1/4 * 1/4 | 1/1024 |
| 6 | 1/4 * 1/4 * 1/4 * 1/4 * 1/4 * 1/4 | 1/4096 |
If the false match probability is set to 1024 (as used by Texpress), you can see from the above table we need to set k to 5. The reason five is selected is that in order to get a false match we need to have all the search term bits set to one, but not contain the term. Hence if k is five we have a one in 1024 chance that a record descriptor will match incorrectly. If we decrease the bit density to say 12.5% or one bit in eight set, a k value of four is sufficient, as shown in the table below:
|
k |
Probability all bits set to one |
Value |
|---|---|---|
|
1 |
1/8 |
1/8 |
|
2 |
1/8 * 1/8 |
1/64 |
|
3 |
1/8 * 1/8 * 1/8 |
1/512 |
|
4 |
1/8 * 1/8 * 1/8 * 1/8 |
1/4096 |
It is easy to see that if we decrease the bit density (d), we also decrease the value of k. We can express the relationship between k, f and d as:
f = (100 / d)k
With a bit of mathematics we can isolate k from the above formula, giving:
k = log(f) / log(100 / d)
Now that k is calculated we can use it to work out the value of b (the length of the bit string). We need to introduce one new variable in order to calculate b:
|
i |
The number of indexed atoms per record defines how many values are to be encoded into the record descriptor. In our example the value of i is five as we have five terms encoded in the record descriptor ( |
Using the value of i we can calculate the value of b. Using a simplistic approach we could take the value of k (bits to set per term) and multiply it by i (number of terms) to get the number of bits set to a 1. If we assume d (bit density) of 25%, we need to multiply the number of 1s set by four to get the value of b. Expressed as a formula, this is (i * k * (100 / d)). Using our example we would have:
5 * 5 * (100 / 25) = 100 bitsSo for our sample record we would have the following configuration:
|
Variable |
Description |
Value |
|---|---|---|
|
f |
False match probability |
1024 |
|
d |
Bit density |
25% |
|
i |
Indexed terms per record |
5 |
|
k |
Bits set per term |
5 |
|
b |
Length of bits string (in bits) |
100 |
In fact the formula used to calculate b is a bit simplistic. It is useful as an approximation, however it is not completely accurate. When we build the record descriptor for a record we use the pseudo random number generator to compute k bits per term. If we have i terms, we call the pseudo random number generator i times, once for each term. Each term will set k/b bits. Thus for each term the probability that a bit is still zero is (1 - k/b), so for i terms the probability that a bit is still zero is (1 - k/b)i. From this the probability that a bit is therefore 1 must be (1 - (1 - k/b)i). We also know the probability of a bit being 1 must be (d / 100), that is the number of one bits based on the bit density. So we end up with:
1 - (1 - k/b)i = d / 100
Now with a bit of mathematics we can isolate b from the above formula, giving:
b = k / (1 - exp(log((100 - d) / 100) / i))
Using the above formula for b with our example record we end up with a value of 90 bits rather than the 100 calculated using the simplistic method. If you did not understand the way b was calculated, it is not important, except to say that Texpress uses the latter formula when determining b. Now that we have the key concepts in place and have examined the variables used to calculate the number of bits to set per term (k) and the length of the bit string (b) we need to consider what we mean by Two Level when we talk about a Two Level Superimposed Coding Scheme for Partial Match Retrieval.
As you can imagine, an indexing scheme that is two level must have two parts to it and, in fact, this is the case. Fortunately the two parts are very similar with both parts using the theory covered in the last section. The first level is the segment descriptor level and the second is the record descriptor level:
|
Segment Descriptor |
A segment descriptor is a bit string that encodes information for a fixed number of records. It uses the theory discussed above, except that a single segment descriptor describes a group of records rather than a single record. The number of records in a segment is part of the system configuration and is known as Nr. A typical value for Nr is around 10. Segment descriptors are stored sequentially in the |
|
Record Descriptor |
The record descriptor level contains one record descriptor per record. Record descriptors are grouped together into lots of Nr with the lots stored one after another in the |
The table below shows the relationship between segment descriptors and record descriptors where Nr is 4:
|
Segment Descriptor 1 |
Record Descriptor 1 |
|
Record Descriptor 2 |
|
|
Record Descriptor 3 |
|
|
Record Descriptor 4 |
|
|
Segment Descriptor 2 |
Record Descriptor 5 |
|
Record Descriptor 6 |
|
|
Record Descriptor 7 |
|
|
Record Descriptor 8 |
|
|
… |
… |
The segment descriptors are consulted first when a search is performed. For every matching segment descriptor the corresponding Nr record descriptors are checked to find the matching record(s). For each segment descriptor that does not match, the associated Nr record descriptors can be ignored. In essence we end up with a scheme that can very quickly discard records that do not match, leaving those that do match.
Calculating a value for Nr
It may be tempting to set the number of records in a segment to a very large number. After all if the segment descriptor does not match, it means Nr records can be discarded quickly. To a point this is correct. However the larger the number of records per segment, the higher the probability that a given segment will contain a match. For example, let's say we have 100 records per segment. The data for 100 records is encoded in each segment descriptor and record descriptors are grouped in lots of 100. Now let's assume we have 500 records in our database and we are searching for a term that will result in one match. It is clear in this case that only one segment descriptor will match (assuming no false matches), so we need to search through 100 record descriptors to find the matching record. If the number of records per segment was 10, we would still get one match at the segment level, however we would only need to look through 10 record descriptors to find the matching record.
Setting the number of records per segment trades off discarding a large number of records quickly (by setting the value high) against the time taken to search the record descriptors in a segment if the segment matches (setting the value low). Also, multi-term queries need to be considered. Since a segment descriptor encodes terms from a number of records, a multi-term query that contains all the query terms spread across the records in the segment will match at the segment level, forcing the record descriptors to be checked. For example, if the search terms were red and house and the first record in a segment contained the word red, while the third record contained the word house, then the segment descriptor would match (as it encodes both words). The record descriptors are then consulted to see if any records contain both terms. Since a matching record does not exist in the segment, time has been "wasted" looking for a non-existent match.
When determining the best value for the number of records in a segment it is important to understand how the database will be queried. In particular, if a lot of single term searches are expected, it makes sense to have a reasonably large number of records per segment (say around 20-50). If multi-term searches are used and the search terms are either related or distinctive (that is, they do not occur in many records), the value may also be high. For example, the Taxonomy module consists mainly of related terms (the Classification Hierarchy). If someone searches for a genus-species combination, it is highly likely that the two terms will appear in the one record (since a species is a narrower term of a genus).
If, however, multi-term queries will contain common non-related terms, a smaller value for records per segment is required. For example, the Parties module contains records that have many common terms. Consider searching for all artists in London (that is Role=artist and City=London). There are probably a lot of records where the role field contains artist, similarly many records may have a City value of London. However, there may not be many records that contain both terms. If the number of records per segment is set high, a large number of segment matches will occur (because at least one record in the segment has a Role of artist and at least one other record in the segment has a City value of London). In this case it is better to set the number of records per segment to be low, say around 10. The Texpress configuration facility will use a value close to 10 for the number of records per segment as this provides a general purpose index without knowledge of the data and expected queries.
There is one other variable used when determining the number of records in a segment and that is the system blocksize:
|
blocksize |
The blocksize is the number of bytes that are read or written at one time when a filesystem is accessed. All filesystem disk accesses occur using this fixed number of bytes. Even if you read one byte, the underlying filesystem will still read blocksize bytes and return the single byte to you. The blocksize of a filesystem is defined when the filesystem is created. Common blocksizes are 1024, 4096 or 8192 bytes. Texpress assumes a default blocksize of 4096 bytes. |
In order to provide efficient searching it is important to ensure that all disk activity occurs in multiples of the filesystem blocksize. So, when selecting the number of records in a segment we need to make sure that the value selected fills an integral number of blocks. If we use our example, we saw that the value for b (length of the bit string) was 90 bits or 12 bytes (rounding up). If we have a blocksize of 4096 bytes, we can fit 341 (4096/12 rounded down) record descriptors in one disk block. So for our sample data the value for Nr would be 341. As our example has only five terms in it this leads to a very high value. In practice, records contain many more terms so the number of records per segment is generally around 10 by default.
Bit Slicing
The final piece of the indexing puzzle is the use of bit slicing to provide a fast mechanism for searching the segment descriptor file. As discussed, a segment descriptor encodes information from Nr records into one descriptor. The descriptors are stored one after the other in the seg file in the database directory. When a query is performed the first step is to search each segment descriptor AND-ing it with the query segment descriptor to see if it matches. When we get a match we then check the record descriptors in the same way. The problem with this approach is that the seg file can be very large and searching through it sequentially can take some time. The diagram below shows a series of segment descriptors and a query descriptor used for searching:
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
… |
(Segment Descriptor 1) |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
… |
(Segment Descriptor 2) |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
… |
(Segment Descriptor 3) |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
… |
(Segment Descriptor 4) |
|
… |
|
|
|
|
|
|
|
|
|
|
(Segment Descriptor N) |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
… |
(Arbitrary Query Segment Descriptor) |
It may be obvious from the table above that in order for a segment descriptor to match the query segment descriptor it requires a 1 bit in each position that the query descriptor has a 1 bit. The other bits in the descriptor are irrelevant. Using this piece of information the fastest way to determine what segment descriptors match is to read slices of the segment descriptors. Where the query segment descriptor has a 1 bit we read a slice (that is one bit from each segment descriptor). The slice is represented by the yellow area enclosed within the lines in the diagram. If we read a slice for each query descriptor 1 bit and AND them together, any resulting 1 bit must contain the position of a segment descriptor that has all 1 bits set as well. In the example above only segment descriptor 1 matches the query segment descriptor.
The problem with this approach is that reading individual bits from a filesystem is extremely inefficient. You may notice however that if we "flip" the segment descriptor file on its side, each slice can now be read with one disk access. The table below shows the segment descriptors "flipped":
|
1 |
0 |
1 |
0 |
… |
|
0 |
1 |
1 |
0 |
… |
|
1 |
0 |
1 |
0 |
… |
|
1 |
1 |
0 |
1 |
… |
|
0 |
0 |
0 |
1 |
… |
|
1 |
0 |
0 |
0 |
… |
|
1 |
1 |
0 |
0 |
… |
|
0 |
1 |
1 |
1 |
… |
|
1 |
0 |
0 |
1 |
… |
|
0 |
0 |
1 |
0 |
… |
If we take the slices we need to check and AND them, then where a 1 bit is set in the resulting slice that segment number matches the query segment descriptor:
|
1 |
0 |
1 |
0 |
… |
AND |
|
1 |
1 |
0 |
0 |
… |
|
|
1 |
0 |
0 |
0 |
… |
|
From our original configuration we know that we set k bits per term, so if a single term query is performed we need to read k bit slices to determine what segments match the query. The bit slicing of the segment file is the reason why Texpress has exceptional query speed.
One issue with bit slicing the segment descriptor file is that in order to store the bit slices sequentially we need to know the length of a bit slice. We know the length of the segment descriptor, it is b, so b bit slices are stored in the file; but what is the length of each slice? In order to determine the length of a bit slice we need to know the capacity of the database, that is how many records will be stored. Using the number of records per segment (Nr) we can calculate the number of segments required; we use the symbol Ns to represent this number. So:
Ns = capacity / Nr
Thus the length of a bit slice in bits is Ns.
False match probability
When the false match probability was introduced it was defined as the number of descriptors to be examined to get one false match. So a value of 1024 is interpreted as the probability of one false match every 1024 descriptors examined. Using this measure is not very useful when configuring a Texpress database because the probability is tied to the capacity of the table rather than the descriptors examined when searching. In order to address this issue the false match probabilities used by Texpress are altered to reflect the probability of a false match when searching the segment file and the probability of a false match in a segment when searching the record descriptor file. In order to make these adjustments the following formulae are used:
Probability of a segment level false match = 1 / (fs * Ns)
Probability of a segment false match = 1 / (fr * Nr)
If we look at the first formula we can see that the probability of a false match at the segment level has changed from one every fs descriptors to one every fs searches. The change removes the number of segment descriptors from the equation. By doing so, fs is now a constant value regardless of the number of segment descriptors. A similar change was made to the false match probability for record descriptors. The number of records per segment was introduced so that the probability is now the number of segments examined before a false match, rather than the number of records.
We have spent a good deal of time looking at the fundamentals of the Texpress indexing mechanism. There is one variable however that requires further investigation as it plays a large part in the automatic generation of configuration values. The variable is the number of indexed atoms per record (is and ir).
An atom is a basic indexable component. Each atom corresponds to one searchable component in the Texpress indexes. What an atom is depends on the type of the data field. The table below shows for each supported data type what constitutes an atom:
|
float integer |
A single numeric value is an atom. |
|
date |
Every date value consists of three components (year, month, day). Each filled component is an atom. For example, if a date field contains |
|
time |
As for dates, time values consist of three components (hour, minute, second). Each component that has a value is an atom. For example, a time value of |
|
latitude |
Latitude and longitude values consist of four components (degree, minute, second, direction). Each component with a value is an atom. For example, a latitude of |
|
string |
A string value (rarely used in EMu) is a text based value that is indexed as one atom. The data value has all punctuation removed and the resulting string forms one component. For example, a string value of " |
|
text |
For text based data each unique word in the text constitutes an atom. A word is a sequence of alphabetic or numeric characters delimited by punctuation (character case is ignored). For example, a text value of " |
If a column can contain a list of values, the number of atoms is the sum of the atoms for each individual value, with duplicate atoms removed. So, if you have an integer column that accepts multiple values and the data is 10, 12, 14 and 12, the number of atoms is three (as 12 is duplicated).
The table above reflects what an atom is for the standard data types used by Texpress. Texpress does, however, provide extra indexing schemes that provide different searching characteristics. The table below details what constitutes an atom for each of these additional indexing schemes:
|
Null Indexing |
Null indexing provides fast searching when determining whether a column contains a value or is empty (that is for *, !*, + and !+ based wildcard searches). It is available for all data types. There is one atom per column for all columns that have null indexing enabled, regardless of whether they contain multiple values, a single value or are empty. |
|
Partial Indexing |
Partial indexing provides fast searching where the search term specifies leading letters followed by wildcard characters (e.g.
If we are providing partial indexing for one and three characters, the one character atoms are:
and the three character atoms are:
So the number of atoms for partial indexing in the above example is four. For columns that contain multiple text values the number of atoms is the sum of the atoms per text value with duplicate atoms removed. |
|
Stem Indexing |
Stem indexing provides searching for all words that have the same root word. This allows users to find a word regardless of the form of the word (e.g. searching for |
|
Phonetic Indexing |
Phonetic indexing provides searching for words that sound similar, that is they contain the same sound groups (e.g. |
|
Phrase Indexing |
Phrase indexing provides fast searching for phrased based searches, that is, searches where the query terms are enclosed within double quotes (e.g. "
Each of these combinations is an atom, however EMu only sets one bit to provide phrase based searching, rather than the normal k bits. |
Now that we have an understanding of what an atom is, we need to look at how Texpress computes the number of atoms in a record.
When explaining the configuration variables used to configure a Texpress table, the number of atoms per record (i) was glossed over. The working example used a value of five based on the data found in a single record. In fact, arriving at a value for the number of index terms per record can be quite involved. It also turns out that the value chosen has a large impact on the overall configuration of the system (which is to be expected as it plays an important part in the calculation of b (length of the descriptor in bits)). Texpress 8.2.01 introduced changes to the indexing system that track dynamically the number of atoms per record. Using these changes Texpress can provide very good configurations regardless of the distribution of the number of atoms per record.
How does Texpress decide on the number of atoms per record? First we need to examine what is the number of atoms in a record for any given record. Based on the previous section (What is an atom?) the number of atoms in a given record consists of three numbers:
|
terms |
The number of terms for which k bits are set when building the descriptor. Most atoms fall into this category. |
|
extra |
The number of extra atoms where two bits are set for the complete word. Extra atoms result from stem and phonetic searching. |
|
adjacent |
The number of adjacent atoms where a combination of two words are indexed together resulting in one bit being set. |
Let's consider an example. If we have a record with one text field with stem based indexing enabled and it contains the text I like lollies do you?, then the breakdown of atoms is:
|
Index Type |
Count |
Bits Set |
Atoms |
|---|---|---|---|
| terms | 5 | k | i, like, lollies, do, you |
| extras | 5 | 2 | i, lik, lol, do, you |
| adjacent | 4 | 1 | i-like, like-lollies, lollies-do, do-you |
In order to arrive at the number of atoms for the record we need to compute a weighted number of atoms based on the number of bits set. The formula is:
i = (terms * k + extra * 2 + adjacent * 1) / k
So using our example and assuming that k=5, the number of atoms for the sample record is (5 * 5 + 5 * 2 + 4 * 1) / 5 or 8 (rounded up). Since we have two values for the number of bits to set per indexed term (ks and kr for segment descriptors and record descriptors respectively) we end up with two weighted values for the number of atoms: one for the segment level (is) and one for the record level (ir).
As you can imagine it could be quite time consuming working out the number of atoms in a record for every record in a table. Texpress makes this easy by storing the three numbers required to determine i with each record descriptor. When a record is inserted or updated the counts are adjusted to reflect the data stored in the record. Using texanalyse the atoms for each record can be viewed. The -r option is used to dump the raw counts:
texanalyse -r eparties
Terms,Extra,Adjacent,RecWeighted,SegWeighted
118,9,14,123,122
126,10,21,132,131
102,3,2,103,103
139,12,39,148,146
130,12,28,137,136
138,15,36,147,145
136,15,36,145,143
…
The first three columns of numbers correspond to the number of terms, extra and adjacent atoms. The last two numbers are the weighted number of atoms for the record descriptor level (ir) and the segment descriptor level (is) respectively. These numbers are the raw input used by Texpress to determine the overall number of atoms to use for configuration.
One approach for arriving at the number of atoms to use for configuration is to take the average of the weighted number of atoms in each record. In this instance a certain percentage of records would be below the average value and the rest above. For records with the average value the bit density of the generated descriptors will be d (25% by default). For records with less than the average number of atoms, the bit density will be less than d, and for those greater than the average, the bit density will be greater than d. From our initial calculations:
k = log(f) / log(100 / d)
We need to maintain the bit density (d) at about 25%, given that k is fixed, otherwise the false match probability drops and false matches are more likely. We need to ensure that the vast majority of records have a bit density of 25% or less. In order to achieve this we cannot use the average number of atoms per record, rather we need to select a higher value.
If we calculate the average number of atoms per record and know the standard deviation, we can use statistical analysis to determine a value for the number of atoms that ensures that most records are below this value (and so the bit density is below 25%). If the number of atoms in each record follows a normal distribution, which is generally the case when the data comes from one source, then analysis shows that 95.4% of records will have a number of atoms value less than the average plus two times the standard deviation, and 99.7% of records will have a number of atoms value less than the average plus three times the standard deviation. Calculating the standard deviation for the number of atoms in each record could take some time so fortunately texanalyse can be used to determine the value. If texanalyse is run without options the following output is displayed:
texanalyse eparties
Analysis of Indexed Atoms per Record
====================================
+---------+---------+---------+
| Atoms | Records | Records |
| | (Rec) | (Seg) |
+---------+---------+---------+
| 93 | 0 | 1 |
| 94 | 1 | 0 |
| 95 | 0 | 3 |
| 96 | 3 | 2 |
| 97 | 2 | 0 |
| 98 | 3 | 3 |
| 99 | 8 | 8 |
| 100 | 0 | 2 |
| 101 | 3 | 1 |
| 102 | 1 | 1 |
| 103 | 13 | 15 |
| 104 | 2198 | 2223 |
| 105 | 966 | 976 |
| 106 | 43 | 290 |
| 107 | 288 | 94 |
…
| 397 | 0 | 0 |
| 398 | 1 | 0 |
+---------+---------+---------+
Record Level Analysis
=====================
Total number of records : 50046
Total number of indexed terms : 6169873
Average number of indexed terms : 123.3
Standard deviation : 18.5
Records <= average : 32726 (65.4<= 123.3)
Records <= average + 1 * standard deviation: 46156 (92.2<= 141.8)
Records <= average + 2 * standard deviation: 48310 (96.5<= 160.4)
Records <= average + 3 * standard deviation: 49114 (98.1<= 178.9)
Records <= average + 4 * standard deviation: 49456 (98.8<= 197.4)
Records <= average + 5 * standard deviation: 49638 (99.2<= 215.9)
Records <= average + 6 * standard deviation: 49732 (99.4<= 234.5)
Records <= average + 7 * standard deviation: 49838 (99.6<= 253.0)
Records <= average + 8 * standard deviation: 49938 (99.8<= 271.5)
Records <= average + 9 * standard deviation: 49990 (99.9<= 290.1)
Records <= average + 10 * standard deviation: 50014 (99.9<= 308.6)
Records <= average + 11 * standard deviation: 50027 (100.0<= 327.1)
Records <= average + 12 * standard deviation: 50036 (100.0<= 345.7)
Records <= average + 13 * standard deviation: 50038 (100.0<= 364.2)
Records <= average + 14 * standard deviation: 50044 (100.0<= 382.7)
Records <= average + 15 * standard deviation: 50046 (100.0<= 401.3)
Segment Level Analysis
======================
Total number of records : 50046
Total number of indexed terms : 6112301
Average number of indexed terms : 122.1
Standard deviation : 17.8
Records <= average : 32744 (65.4<= 122.1)
Records <= average + 1 * standard deviation: 46163 (92.2<= 139.9)
Records <= average + 2 * standard deviation: 48306 (96.5<= 157.7)
Records <= average + 3 * standard deviation: 49126 (98.2<= 175.5)
Records <= average + 4 * standard deviation: 49459 (98.8<= 193.2)
Records <= average + 5 * standard deviation: 49645 (99.2<= 211.0)
Records <= average + 6 * standard deviation: 49728 (99.4<= 228.8)
Records <= average + 7 * standard deviation: 49832 (99.6<= 246.6)
Records <= average + 8 * standard deviation: 49938 (99.8<= 264.4)
Records <= average + 9 * standard deviation: 49989 (99.9<= 282.1)
Records <= average + 10 * standard deviation: 50014 (99.9<= 299.9)
Records <= average + 11 * standard deviation: 50027 (100.0<= 317.7)
Records <= average + 12 * standard deviation: 50036 (100.0<= 335.5)
Records <= average + 13 * standard deviation: 50038 (100.0<= 353.2)
Records <= average + 14 * standard deviation: 50044 (100.0<= 371.0)
Records <= average + 15 * standard deviation: 50046 (100.0<= 388.8)
The table under the Analysis of Indexed Atoms per Record heading shows for a given number of atoms (in the Atoms column) how many records have that number of atoms at the record level (Records (Rec)) and segment level (Records (Seg)). The Record Level Analysis and Segment Level Analysis summaries show the average number of atoms and standard deviation for each level. The table below the standard deviation shows the number of records less than the average plus a multiple of the standard deviation. The first number in the brackets is the percentage of records below the value and the number after the equal sign is the number of atoms. For example, if you take the line:
Records <= average + 3 * standard deviation: 49126 (98.2<= 175.5)this indicates that 49126 records are below the average plus three times the standard deviation, which represents 98.2% of the records. The number of atoms represented by the average plus three times the standard deviation is 175.5. Using this table it is possible to determine what would be good values for is and ir. Remember that we want most records to be below the selected value, in most cases over 98%. Using this as a guide, for the above output a suitable value for ir would be 180 (178.9 rounded up) and for is 175 (175.5 rounded down). While these may seem to be good values at first glance, it is worth considering the uppermost extremes as well. For the record level analysis the maximum number of atoms in a record is 398. If we use a value of 180 for the number of atoms at the record level, this means that the record with the maximum number of atoms sets 2.2 times the number of bits than a record with 180 atoms. If we apply this to the bit density, this corresponds to a bit density of 55% (25% * 2.2). If we are using 5 as the value for k (five bits set per atom), then the false match probability for the record with 398 atoms is:
(55/100)5 ≈ 0.05 or 1/20 Thus the record with 398 atoms has a false match probability of 1/20 rather than the required 1/1024. In general this is an acceptable value provided there are not many records with this high probability. If, however, the bit density is over 75% for the record with the maximum number of atoms, it may be worth increasing the value of i so that the density is lowered (by making i about one third of the value of the maximum number of atoms). In general, this is only required in extreme cases and tends to arise only where a large number of data sources are loaded into one table.
The idea of adding a number of standard deviations to the average number of atoms provides us with our last variable:
|
v |
The number of standard deviations to add to the average number of atoms per record to determine the value of i, commonly called the variance. Since we have a segment and a record level value for i we also have a segment and record level value for v. The default value for the segment level is 2.0, and for the record level 3.0; that is, we add in two times the standard deviation to calculate the value of is and three times the standard deviation to calculate ir. |
It may be opportune at this time to summarize the variables used as part of the configuration of a Texpress database. As Texpress uses a two level scheme, there are two sets of variables, one for the segment level and one for the record level. The variables with an r subscript apply to record descriptors, while those with an s subscript are used for segment descriptors:
|
Variable |
Description |
Default value |
|---|---|---|
| Ns | Number of segment descriptors | Calculated from capacity |
| Nr | Number of record descriptors per segment | Calculated with minimum of 10 |
| kr | Bits to set per term in record descriptor | Calculated |
| ks | Bits to set per term in segment descriptor | Calculated |
| br | Bit length of a record descriptor | Calculated |
| bs | Bit length of a segment descriptor | Calculated |
| fr | False match probability for record descriptors | 1024 |
| fs | False match probability for segment descriptors | 4 |
| dr | Bit density of record descriptors | 25% |
| ds | Bit density of segment descriptors | 25% |
| ir | Indexed terms per record descriptor | Calculated from data |
| is | Indexed terms per segment descriptor | Calculated from data |
| vr | Number of standard deviations to add to average at record level | 3.0 |
| vs | Number of standard deviations to add to average at segment level | 2.0 |
| blocksize | Filesystem read / write size in bytes | 4096 |
Texpress2 has a number of tools that provide detailed information about the indexing mechanism. Three programs are provided, where each focuses on one aspect of system configuration:
- texanalyse provides information about the number of atoms per record.
- texdensity shows the actual bit density for each segment and record descriptor.
- texconf generates values for calculated configuration variables (k, b, Nr and Ns).
The texanalyse tool allows information about the number of atoms per record to be obtained. It supports both the record level and segment level. The primary use of texanalyse is to check that the value used for the number of atoms per record (i) is suitable: in particular to check the records with the maximum number of atoms per record are within an acceptable range of i. We define acceptable as within three times the value of i when a bit density (d) of 25% is used. It is also instructive to use texanalyse to produce the raw data that can be fed to spreadsheet programs for analysis. The usage message is:
Usage: texanalyse [-R] [-V] [-c|-r] [-s] dbname
Options are:
-c print analysis in CSV format
-r print raw data in CSV format
-s suppress empty rows
If the raw atom data per record is required, the -r option is used:
texanalyse -r eparties
Terms,Extra,Adjacent,RecWeighted,SegWeighted
118,9,14,123,122
126,10,21,132,131
102,3,2,103,103
139,12,39,148,146
…
The output is in CSV (comma separated values) format suitable for loading into a spreadsheet or database. The data contains the number of term atoms, extra atoms and adjacent atoms for each record in the table. The weighted number of atoms for the record and segment level is also given.
It is also possible to export in CSV format the number of records at both the record and segment levels that have a given number of atoms:
texanalyse -c eparties
Atoms,RecRecords,SegRecords
101,3,1
102,1,1
103,13,15
104,2198,2223
105,966,976
106,43,290
107,288,94
108,93,19
109,536,527
110,15,13
111,6,20
…
The output can be loaded into spreadsheet programs for analysis. The graph below shows the number of records for each atom count from the above output at the record level:
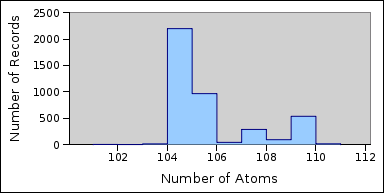
Producing a graph of the number of records with each atom count provides a useful mechanism for determining how close the distribution of the number of atoms in a record is to a normal distribution. In particular it can be used to see whether loading separate data sources has resulted in a number of normal distributions being overlaid (one per data source). The graph at the start of this article shows clearly that at least three separate data sources were loaded into the Parties table.
The final use for texanalyse is to produce a summary detailing the average number of atoms per record and the standard deviation. A list of the average plus an integral number of standard deviations is also shown:
texanalyse elocations
Analysis of Indexed Atoms per Record
====================================
+---------+---------+---------+
| Atoms | Records | Records |
| | (Rec) | (Seg) |
+---------+---------+---------+
| 49 | 17 | 17 |
| 50 | 0 | 0 |
…
| 106 | 0 | 1 |
+---------+---------+---------+
Record Level Analysis
=====================
Total number of records : 1419
Total number of indexed terms : 90309
Average number of indexed terms : 63.6
Standard deviation : 9.4
Records <= average : 1170 (82.5<= 63.6)
Records <= average + 1 * standard deviation: 1244 (87.7<= 73.1)
Records <= average + 2 * standard deviation: 1313 (92.5<= 82.5)
Records <= average + 3 * standard deviation: 1323 (93.2<= 91.9)
Records <= average + 4 * standard deviation: 1418 (99.9<= 101.4)
Records <= average + 5 * standard deviation: 1419 (100.0<= 110.8)
Segment Level Analysis
======================
Total number of records : 1419
Total number of indexed terms : 91805
Average number of indexed terms : 64.7
Standard deviation : 9.8
Records <= average : 1167 (82.2<= 64.7)
Records <= average + 1 * standard deviation: 1243 (87.6<= 74.5)
Records <= average + 2 * standard deviation: 1311 (92.4<= 84.3)
Records <= average + 3 * standard deviation: 1323 (93.2<= 94.1)
Records <= average + 4 * standard deviation: 1417 (99.9<= 103.9)
Records <= average + 5 * standard deviation: 1419 (100.0<= 113.7)
The analysis tables at the end can be used to determine whether the computed number of atoms per record is suitable. The computed record level value is the average plus three times the standard deviation and the segment value is the average plus two times the standard deviation. The standard check is to ensure that the maximum number of atoms is less than three times the value chosen for i (assuming a bit density (d) of 25%).
In order to test the effectiveness of a configuration it is useful to be able to determine the bit density for all segment and record descriptors. The texdensity utility provides this functionality. The usage message is:
Usage: texdensity [-R] [-V] [[-cr|-cs] | [-dr|-ds]] [-s] [-nrn -nsn] dbname
Options are:
-cr print record descriptor density in CVS format
-cs print segment descriptor density in CVS format
-dr print record descriptor density
-ds print segment descriptor density
-s suppress empty values
-nrn scan n record descriptors
-nsn scan n segment descriptors
If some analysis of the bit density is required, the -cr or -cs option can be used to output in CSV format the number of bits set and the bit density per record or segment descriptor respectively:
texdensity -cr elocations
Index,Bits,Total,Density
0,424,2384,17.79
1,405,2384,16.99
2,404,2384,16.95
3,438,2384,18.37
…
The Index column is the record descriptor index (or segment descriptor index if -cs is used). The number of bits set is next, followed by the total number of bits that could be set and finally the bit density as a percentage. In general the bit density should be below the default value of 25%.
It is also possible to get the average bit density, the standard deviation and the maximum bit density:
texdensity -ds elocations
Segment descriptor analysis
===========================
Descriptor Bits set Total bits Density
+----------+----------+----------+----------+
| 0 | 1193 | 17280 | 6.90 |
| 1 | 1164 | 17280 | 6.74 |
| 2 | 1007 | 17280 | 5.83 |
| 3 | 971 | 17280 | 5.62 |
…
| 135 | 0 | 17280 | 0.00 |
+----------+----------+----------+----------+
Number of descriptors : 119
Average density : 4.42
Standard deviation : 1.10
Maximum density : 10.39
The output above shows the summary for the segment descriptors of the elocations table. As the maximum density of 10.39 is well below the 25% density required, this indicates that the value for the number of atoms per record can be lowered. The computed number of atoms per record at the segment level was 83. If we lower the number of atoms per record proportionally (83 * 10.39 / 25), the number of atoms to use is 34. After reconfiguring the number of atoms per record at the segment level to 34, the following density summary was found:
Number of descriptors : 119
Average density : 10.45
Standard deviation : 2.44
Maximum density : 23.37
Based on this output the number could be lowered further as the average bit density is 10.45 and if we add three times the standard deviation, we get 17.77 (10.45 + 3 * 2.44), which is still well below 25%. The reason segment descriptor bit densities are generally lower than record descriptor densities is due to the repeating of atoms in all the records that make up the segment descriptor. In particular, there are a number of fields in EMu that contain the same value for all records in a segment (e.g. Record Status, Publish on Internet, Publish on Intranet, Record Level Security, etc.). Since every record in the segment has the same value in these fields we should only count the atom once, however Texpress does not have any mechanism available for tracking how many atoms are repeated in a segment, so a worst case scenario is assumed where no atoms are repeated. In general this results in segment descriptor files that are larger than they need to be. Apart from using more disk space, the searching mechanism is not affected overtly as bit slices are read rather than complete segment descriptors. It is possible to adjust the number of atoms per record at the segment level, resulting in some cases with substantial savings in disk space.
The next section on setting configuration parameters details how this is set.
The texconf utility is a front end program to the Texpress configuration facility. Using texconf it is possible to alter any of the configuration variables and see the effect it has on the final configuration (that is the values of Nr, Ns, br, bs, kr and ks). The usage message is:
Usage: texconf [-R] [-V] [-bn] [-cn] [-drn] [-dsn] [-frn] [-fsn] [-mn] [-irn -isn|-nrn -nsn -vrn -vsn] dbname
Options are:
-bn filesystem blocksize of n bytes
-cn capacity of n records
-drn record descriptor bit density of n
-dsn segment descriptor bit density of n
-frn record descriptor false match probability of n
-fsn segment descriptor false match probability of n
-mn minimum number of records per segment of n
-irn record descriptor indexed terms per record of n
-isn segment descriptor indexed terms per record of n
-nrn scan n records to determine -ir value
-nsn scan n records to determine -is value
-vrn increase -ir value by n standard deviations
-vsn increase -is value by n standard deviations
A close look at the options will show that most correspond to the variables discussed in this article. Using the options you can test the effect of changing variables. Running texconf without any options will generate a configuration based on the default values using the current database capacity:
texconf elocations
Index Configuration
===================
Capacity of database (in records) : 1632
Number of segments (Ns) : 136
Number of records per segment (Nr) : 12
Words per segment descriptor : 540
Words per record descriptor : 79
Bits set per indexed term (segment) : 5
Bits set per indexed term (record) : 7
Record Descriptor Configuration
===============================
Records scanned to determine indexed terms : 1419
Average number of indexed terms : 63.6
Standard deviation of indexed terms : 9.4
Standard deviations to increase average : 3.0
Expected number of indexed terms : 92
False match probability : 0.000081 [1 / (1024 * Nr)]
Record descriptor tag length (bits) : 144
Bits set per extra term : 2
Bits set per adjacent term : 1
Segment Descriptor Configuration
================================
Segments scanned to determine indexed terms : 118
Average number of indexed terms : 776.0
Standard deviation of indexed terms : 108.8
Standard deviations to increase average : 2.0
Expected number of indexed terms : 994
Average number of indexed terms per record : 64.7
Standard deviation of terms per record : 9.1
Expected number of indexed terms per record : 82
False match probability : 0.001838 [1 / (4 * Ns)]
Bits set per extra term : 2
Bits set per adjacent term : 1
Index Sizes
===========
Segment size : 4096
Segment descriptor file size : 286.88K
Record descriptor file size : 544.00K
Percent of record descriptor file wasted : 1.56%
Total index overhead : 830.88K
The output is broken up into four areas. The first area (Index Configuration) prints out the generated configuration values. These values can be entered into the Texpress configuration screen. The second area (Record Descriptor Configuration) details the settings used when calculating the record descriptor configuration. The third area (Segment Descriptor Configuration) shows the values used when calculating the segment descriptor configuration. The last area (Index Sizes) indicates the size of the index files required for the generated configuration.
The table below shows where each of the configuration variables can be found:
|
Variable |
Name in texconf |
|---|---|
| Ns | Number of segments (Ns) |
| Nr | Number of records per segment (Nr) |
| bs | Words per segment descriptor (multiply by 32) |
| br | Words per record descriptor (multiply by 32) |
| ks | Bits set per indexed term (segment) |
| kr | Bits set per indexed term (record) |
| is | Expected number of indexed terms [Segment Descriptor Configuration] |
| ir | Expected number of indexed terms [Record Descriptor Configuration] |
| fs | False match probability [Segment Descriptor Configuration] |
| fr | False match probability [Record Descriptor Configuration] |
| vs | Standard deviations to increase average [Segment Descriptor Configuration] |
| vr | Standard deviations to increase average [Record Descriptor Configuration] |
Let's say that after some analysis we decide that the average number of atoms per record at the segment level should really be 34 instead of 82. We can run:
texconf -is34 elocations
Index Configuration
===================
Capacity of database (in records) : 1632
Number of segments (Ns) : 136
Number of records per segment (Nr) : 12
Words per segment descriptor : 222
Words per record descriptor : 79
Bits set per indexed term (segment) : 5
Bits set per indexed term (record) : 7
…
Index Sizes
===========
Segment size : 4096
Segment descriptor file size : 117.94K
Record descriptor file size : 544.00K
Percent of record descriptor file wasted : 1.56%
Total index overhead : 661.94K
Notice how the Words per segment descriptor value has decreased to reflect the lower number of atoms per record. Also the Segment descriptor file size has decreased. Using texconf you can determine the impact on the size of the index files when configuration variables are adjusted.
The final part of this document deals with setting configuration variables on a per database basis so that future configurations will use these values.
This information forms Step 7 in How to optimize Texpress.

